this post was submitted on 23 Aug 2023
67 points (100.0% liked)
196
16503 readers
2392 users here now
Be sure to follow the rule before you head out.
Rule: You must post before you leave.
founded 1 year ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
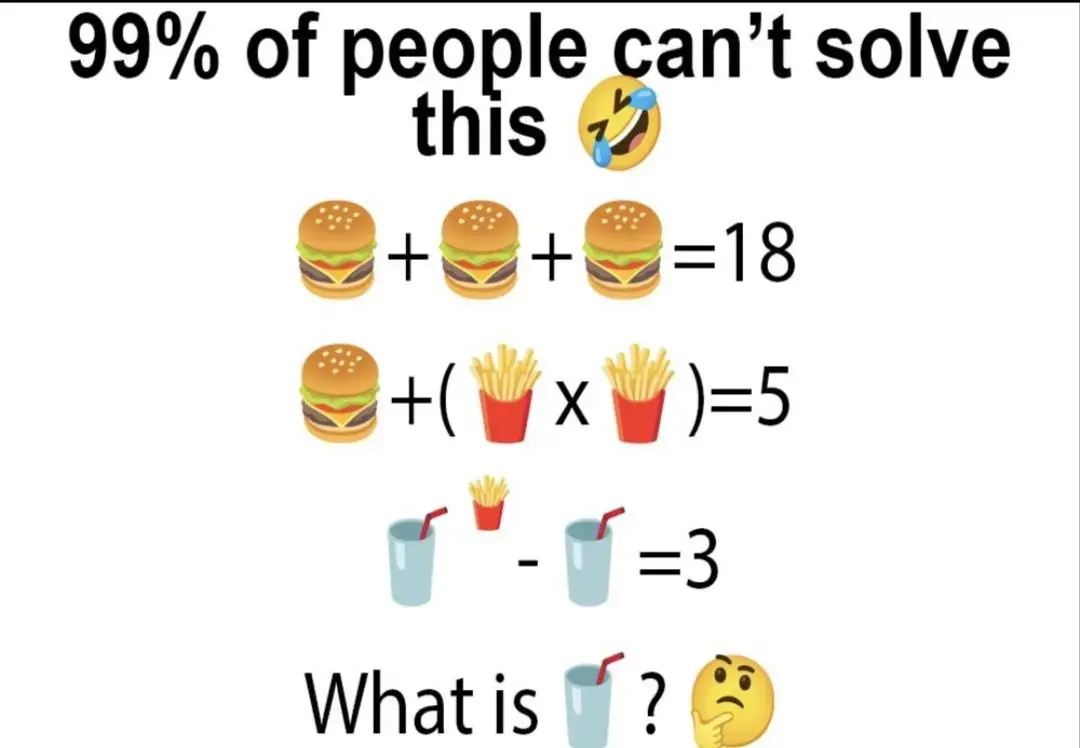
Well let's break it down:
Simple!
Wait, what happened in the second to last bullet point? You can't convert a power like that when subtracting (you can when dividing).
It's like you'd convert "2^4 - 2" into "2^(4-1)", which gives two different results (14 vs 8).
For those curious, I threw 🥤^i - 🥤 = 3 into wolfram.
🥤 ≈ -2.97983 + 0.0388569 i... or 🥤 ≈ 0.27972 - 0.748461 i...
You're right, idk what I was thinking there 😕
I think they're saying no one can give the real answer to this... which is technically true because the answer is imaginary.
you forgot the ± when square rooting:
🍟 = ±i
this is because i × i = -1 and -i × -i = -1
Bah, yes I forgot about that
Don't you mean 🍟 = i?
And just like that, I'm back to junior high grumbling about the concept of imaginary numbers.
Fuck you, y'all made up! 🤣
Lol I didn't quite get my math right, but it still involves imaginary numbers. Fun fact! Any 3D game you've played in the past probably quarter century doesn't just use 1 dimension of imaginary numbers, but 3 to represent 3D rotation! Quaternions are difficult to visualize since it's a 4-dimensional quantity but they're perfect for representing rotation in 3D space without suffering from gimbal lock like rotation matrices.